【学点记点】MVP矩阵

事先说一下，可能由于定义的坐标系不同，不同地方的公式中负责z轴的地方可以看到不同+-符号上的差异，这些都无所谓，因为只要反转z轴，就可以完成左右手坐标系的互换。

模型和世界和摄像机

或许该从坐标系讲起，对于一个物件，一个3d模型资产，它有自己的坐标系 x-y-z，或许以它的中心为坐标原点,我们用以描述模型内部相对位置的这个空间、这个场所——我们称之为 模型空间。

但是一个单独物件很少作为一个场景运作，我们会在一个场景、或者是一个世界里，我们把这一个个模型塞在这个世界里，但是坐标系肯定不是之前以某个模型为中心的坐标系了，我们会重新以某个世界原点建立世界坐标系，我们又在这里描述物件们的相对位置，这个场所——我们称之为 世界空间。

在多考虑一步，世界、模型这些都是他者，有别于此的是主体的视角(这点很重要，我们通过显示器看到的就是这个视角就是摄像机的视角，我们需要这样一个观察者，它有着自己的位置，朝向，还有视野范围，唉 总之 这个场所——我们称之为 观察空间

但是实际上，坐在屏幕前的我们看到的不是这些空间本身，我们透过一个平面的屏幕看到摄像机的传给我们的信息，平面的、经过裁剪过的影像，唉 总之这个、、算是空间吧——我们称之为 裁剪空间

这四个空间是 彼此之间相互转化的一个关系：模型 -> 世界 -> 观察 -> 裁剪

从一个空间到另一个空间的变化伴随着坐标的改变，实际上，这玩意我们通过矩阵运算实现这种变换，如下就是三个矩阵：

• 模型矩阵（Model）
• 观察矩阵（View）
• 投影矩阵（Projection）。

取其首字母，这三个玩意就是MVP矩阵,还挺好记的。

模型空间—M矩阵—世界空间

M矩阵不是一个单一的矩阵，我们描述模型空间的变换往往伴随着 三个操作 缩放、旋转、平移

而这三个操作依次进行的结果就是M矩阵

值得注意的是，我们的矩阵运算是左乘，所以 经过对应的缩放、旋转、平移 之后，我们从空间A变换到空间B：B=M*A

而且这个顺序是不能变的，因为一个物件出现世界，一般都是 在原点，此时缩放、旋转的操作需要一个中心，在不进行移动的时候这个中心在模型和世界空间是重合的，所以先进行这个操作，最后进行平移

• 虽然是x-y-z三个维度，但是你可能发现下面的矩阵形式是四维的，这是因为平移变换不是齐次的，所以额外引入一个维度: 4*4的一个矩阵

$$
\left[
\begin{matrix} 1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & cos \theta & -sin\theta & 0 \\
0 & sin \theta & -cos\theta & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
k_x & 0 & 0 & 0 \\
0 & k_y & 0 & 0 \\
0 & 0 & k_z & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right]
$$

• 值得注意的是，中间这个旋转矩阵的形式是依据你旋转的的轴，比如上面的公式就是绕x轴旋转

世界空间—V矩阵—观察空间

• C=V*B

其实摄像机也只是一个物件，其实可以把这个过程理解为 M矩阵过程的反向，但是摄像机一般没有缩放

• 显然摄像机的视角立足于世界空间，由于涉及旋转中心，所以首先要将世界原点和摄像机移动重合起来，所以是先平移再旋转，但是摄像机不会缩放吧，我们可以把它理解成徒有位置和朝向的单一点，缩放不具备意义，但是再一些引擎中，摄像机的坐标系和世界坐标系不是一个方向（比如unity，所以最后处理的时候会反向z轴，如下

$$
\left[
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & -1 & 0 \\
0 & 0 & 0 & 0
\end{matrix}
\right]
\left[
\begin{matrix}
1 & 0 & 0 & 0 \\
0 & cos \theta & -sin\theta & 0 \\
0 & sin \theta & -cos\theta & 0 \\
0 & 0 & 0 & 1
\end{matrix}
\right] \left[
\begin{matrix} 1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1
\end{matrix}
\right]
$$

观察空间—P矩阵—裁剪空间【这个比较复杂】

• 再观察空间里，我们实际还是三维中的点（虽然是4*4），但是在投影过程中，我们需要把这些三维信息映射到二维屏幕上，但实际上我们P矩阵不是这一步
• D=P*C 得到的D仍旧是一个三维空间，他不是一个最后投影的结果，但是在为投影做准备。裁剪空间的目的是帮助判断顶点是否可见。

我们可以用这种方式理解这个裁剪空间：裁剪空间是一个111的区域，我们需要把视锥体里的内容压缩到这个区域，那除此之外的东西都是我们看不到的，以这种方式进行所谓的裁剪。

一般投影有两种：一种是正交投影、一种是透视投影

前者就是 无论远近，一样大的东西怎么看都是一样的大小

后者则是 我们人眼的 近大远小

为了理解投影，我们需要引入视锥体这一概念: 这是透视摄像机可以看到和渲染的区域的形状

就像一个被切掉了尖端的金字塔，由远近两个平行的矩形接连而成的区域，若是相同，这就成了一个长方体（此时为正交投影）；若是不一样，那就是透视投影

先考虑正交投影吧，我们需要 把一个长方体变换到一个中心位于原点，坐标范围[-1,1]的立方体，因此通过移动加缩放即可完成变换，我们知道本身 视锥体 长方形的 长宽高 ，以及某个点在摄像机空间中的位置，则对于当前长方体的中心点位置就是 （**(r+l)/2,(t+b)/2,(n+f)/2**）,则平移矩阵是

$$
\left[
\begin{array} { l l l l }
1 & 0 & 0 & -\frac{right+left}{2} \\
0 & 1 & 0 & -\frac{top+button}{2} \\
0 & 0 & 1 & -\frac{near+far}{2} \\
0 & 0 & 0 & 1
\end{array}
\right]
$$

然后根据长宽高 进行缩小，由于由于我们本身就是 (r-l)/2,(t-b)/2,(n-f)/2

由于大数减小数还是正的，然后缩小就放大系数的倒数，则缩放系数是

$$
\left[
\begin{array} { l l l l }
\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1
\end{array}
\right]
$$

先平移后缩放，合并一下就是：

$$
\left[
\begin{array} { l l l l }
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\
0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\
0 & 0 & 0 & 1
\end{array}
\right]
$$

这就是正交投影的全部

而透视投影的视锥体近处的矩形和远处的矩形是不一样的，所以我们可以先进行一个类似挤压的操作，把远处的矩形挤压到和近处的一致，经过这一处理之后的视锥体就和正交投影一样了，直接套用正交投影的P矩阵就完事了。

那现在开始专注这个挤压操作，来个图可能比较直观吧

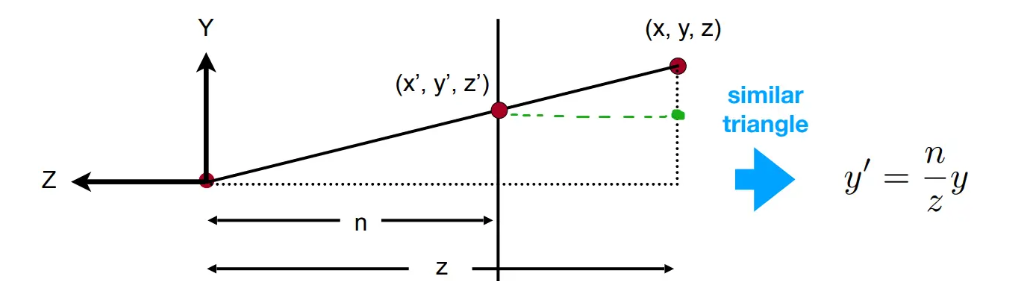
但对于我们举证来讲这个每个点的xyz都只是过客，对于xy的变动，用 n/z = x’ /x

这里等比关系可推理处压缩矩阵的x y 的变换参数，这也是一个类似缩放的齐次变换，

为了好看大家都乘z ，但是经过变换齐次的那个 1 会变成 z ,根据这个规则，我们的最后一行用（0 0 1 0） 就能完成这个变换

现在是这样的：$\left( \begin{array} { l } { n x / z } \\ { n y / z } \\ { unknow } \\ { 1 } \end{array} \right) =>\left( \begin{array} { l } { n x } \\ { n y } \\ { unknow } \\ { z } \end{array} \right)$

但是z轴呢？

其实z轴的缩放和位移我们是不知道的，,但挤压后的某些结果我们是知道的：

• 一个是近平面

  对于本来就是在近平面的点，也就是z为n的点，则经过挤压后其齐次坐标为，下图

$$
\left( \begin{array} l x \ y \ n \ 1\end{array} \right) =>\left( \begin{array} l nx \ ny \ n^2 \ n\end{array} \right)
$$

对于远平面上的也是，但是n变成f, 然后讨论 x ,y 为 0的情况

则我们我们只抽出对z轴产生影响的那行，设缩放为A, 位移为B，则有 $\left( \begin{array} { l l } { 0 } & { 0 } & { A } & { B } \end{array} \right) \left( \begin{array} { l l } { x } \\ { y } \\ { n } \\{ 1 } \end{array} \right) = n ^ { 2 }$ 也就可以得到**A*n+B=n^2**

同理 也有 **A*f+B=f^2 唉 然后联立求解就可以得到： A=n+f ; B=-nf*

我的想法是：所以要这么得到如下的矩阵，是因为本身 这个压缩就是我们制定的规则，所以需要特例点回溯性建构出这个矩阵。那么现在则结果如下

$$
\left[
\begin{array} { l l l l }
n & 0 & 0 & 0\\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}
\right]
$$

然后直接套用上一步的正交投影的矩阵，那透视投影的p矩阵就长这样子了

$$
\left[
\begin{array} { l l l l }
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l} \\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b} \\
0 & 0 & \frac{2}{n-f} & -\frac{n+f}{n-f} \\
0 & 0 & 0 & 1
\end{array}
\right]\left[
\begin{array} { l l l l }
n & 0 & 0 & 0\\
0 & n & 0 & 0 \\
0 & 0 & n+f & -nf \\
0 & 0 & 1 & 0
\end{array}
\right]= \left[
\begin{array} { l l l l }
\frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\
0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\
0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f} \\
0 & 0 & 1 & 0
\end{array}
\right]
$$

$$
\left[
\begin{array} { l l l l }
\frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0 \\
0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0 \\
0 & 0 & \frac{n+f}{n-f} & -\frac{2nf}{n-f} \\
0 & 0 & 1 & 0
\end{array}
\right]
$$

唉 捋一下清晰多了